On Sevenths
Dec
2
2020
As we are homeschooling our 4th grader this year, and as we are starting the fractions section of math, I have been thinking of fractions. In particular, the sevenths.
All other fractions for single-digit denominators made sense to me, regarding converting them to decimals. But not seven.
The closest thing to not making sense other than seven is that 9/9 = 0.999999… and seems to me that 9/9 approaches 1 but never equals it. The difference is 0.0repeating1.
But on to sevenths. I have been telling my son that he needs to know his multiplication facts by heart, and I then thought it odd that I never tried to memorize what 1/7 is. So I set myself to doing it. I must have, long ago, decided it made no sense and was not worth doing, but doing it now it’s not so bad and I don’t know why I took so long to do so.
One seventh is 0.142857 with those 6 digits repeating forever.
For those starting to get bored, here’s where it starts to get interesting, at least for those of us who can find numbers interesting. And if numbers don’t interest you, maybe patterns will?
I wanted to know why those numbers were what they were. I don’t know that I got the why, but it’s making more sense to me now that I looked into it a bit.
Most people’s reactions, judging by stuff written online, is that is it seven doubled, then that doubled, then that doubled plus one more good measure (maybe rouding up).
So 7 doubled is 14, doubled is 28, doubled is 56 but it becomes 57 in this pattern somehow.
There you go: 0.142857142857142857…
But there never was a good explanation for why the 56 got rounded up to 57. Looking into it further, I found a better explanation for that sequence of numbers.
First of all, we need some background information. Namely, the repeating patern of remainders in the 1/7:
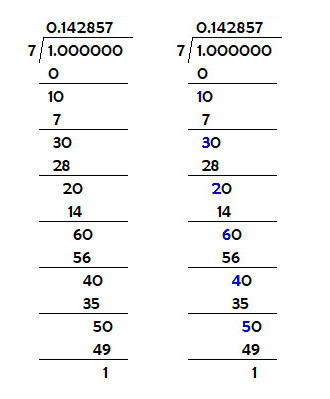
Notice the remainders in the division problem there, highlighted in blue for convenience. It is a repeating pattern of 132645.
Side note: 132645 also could be a firing order of a 6-cylinder engine, and it also is a version of a Gray Code for binary values, assuming it needs only the values 1-6.
Now that we have that established, how does that relate to the actual decimal equivalent of 1/7?
After all, the pattern of 14, 28, 56 is 7 * 2, 7 * 4, and 7 * 8…
But look closer at the pattern. If you double up the numbers, you see the pattern is 14, 42, 28, 85, 57, and 71.
If you assume that all numbers greater than 7*7 are rounded up for some reason, then you see that they are all multiples of 7.
14 is (7*2)*1,
42 is (7*2)*3,
28 is (7*2)*2,
84 is (7*2)*6,
56 is (7*2)*4, and
70 is (7*2)*5
So if you take the multiples of 14 in the order of the remainder values, you get the values of the double-digit numbers in the decimal value.
Also, the numbers over 50 aren’t really rounded up, because they aren’t used. Notice that just the first digits of those values are what’s used for the decimal portion; it all works nicely if you ignore the ones places.
14 is (7*2)*1,
42 is (7*2)*3,
28 is (7*2)*2,
84 is (7*2)*6,
56 is (7*2)*4, and
70 is (7*2)*5
Last little factoid about the sevenths fractions – the pattern progression. Note what happens when you line up the decimal values:
1/7 = 0.142857142
2/7 = 0.285714285
3/7 = 0.428571428
4/7 = 0.571428571
5/7 = 0.714285714
6/7 = 0.857142857
Even though the pattern repeats, it doesn’t line up nicely. So what happens if you line up the pattern nicely, so that the numbers follow the order they are in the decimal, like this?
0.142857142
0.428571428
0.285714285
0.857142857
0.571428571
0.714285714
0.142857142
See how it’s like a scrolling pattern then?
What’s interesting is the fractional values of that order:
0.142857142 = 1/7
0.428571428 = 3/7
0.285714285 = 2/7
0.857142857 = 6/7
0.571428571 = 4/7
0.714285714 = 5/7
To get a nice, visually-pleasing order to the decimal values, you put the fractions in the remainder order.
After all that, I finally was able to memorize the value of 1/7. I just go with the doublings of 7: 14, 28, 56 but not 56 it’s 57 because that last one needs to round up for some reason. That’s the easiest way to remember it, for me at least.
And they shall divide it into seven portions; Judah shall stay in its territory on the south, and the house of Joseph shall stay in their territory on the north.
Joshua 18:5


This little article thingy was written by Some Guy sometime around 6:57 am and has been carefully placed in the Technical category.

 This is Alpha, the first-born, when he was 2YO.
This is Alpha, the first-born, when he was 2YO. This is Beta, the second-born, when he was about 2YO.
This is Beta, the second-born, when he was about 2YO. This is Gamma, the third-born, when he was about 18MO.
This is Gamma, the third-born, when he was about 18MO.


December 2nd, 2020 at 10:19 am
I learned my 7 multiplication table by watching a lot of football on TV.
January 13th, 2021 at 3:02 am
I learned eighths from stock prices, back when they were printed in a newspaper. I recommend them over sevenths; much easier.